Exercise 4.1.8

Exercise statement

Show that the principle of induction (Axiom 2.5) does not apply directly to the integers. More precisely, give an example of a property $P(n)$ pertaining to an integer $n$ such that $P(0)$ is true, and that $P(n)$ implies $P(n{{+}\!{+}})$ for all integers $n$ , but that $P(n)$ is not true for all integers $n$ . Thus induction is not as useful a tool for dealing with the integers as it is with the natural numbers. (The situation becomes even worse with the rational and real numbers, which we shall define shortly.)

Hints

I can’t think of a good hint for this exercise. Try reading the next section paragraph by paragraph (stopping after each paragraph to attempt the exercise again).

How to think about the exercise

Exercises that ask you to find an example come with an associated extra question of “What must the solution space look like?” Is there some simple characterization of every property $P$ that works as a solution to this exercise? Another way to think about this is to ask the following: for any $P$ that is a solution to this exercise, what does $\{n \in \mathbf Z : P(n)\}$ look like? Let’s try to think this through.

First, if $P(0)$ is true, and if $P(n)$ implies $P(n{{+}\!{+}})$ for all integers $n$ , then it must also be the case that $P(n)$ implies $P(n{{+}\!{+}})$ for all natural numbers $n$ . So any $P$ that we give must be true for all natural numbers.

But we also know that $P$ cannot hold for all integers. In other words, we want to find a $P$ that holds for all natural numbers, but where there is also a negative integer $-n$ such $P(-n)$ is false. This is a necessary condition, but not necessarily a sufficient condition. Is it also a sufficient condition? It is not: consider $P(n)\equiv$ “ $n$ is not equal to $-1$ ”. This is true for all natural numbers and fails for $n=-1$ , but it also fails the inductive hypothesis, since for $n=-2$ , we see that $P(n)$ does not imply $P(n{{+}\!{+}})$ .

So we want some stronger necessary condition, which we hope will also be a sufficient condition. It’s not obvious what thought to think next. So let’s just think concretely. We already know $P(0), P(1), \ldots$ must all be true. What about $P(-5)$ ? Well, that could be true or false. What if it’s true? Then the inductive hypothesis says that $P(-4)$ is true, so $P(-3)$ must be true, and so on. Once we get to $P(0)$ , we already know that the rest is true. What if $P(-5)$ is false? Could $P(-6)$ be true? No, because if $P(-6)$ then the inductive hypothesis tells us $P(-5)$ is true! So if $P(-5)$ is false, then $P(-6)$ is also false, which means $P(-7)$ is also false, and so on.

Generalizing the previous paragraph, let $m$ be an integer. If $P(m)$ is true, then the inductive hypothesis says that $P(m+1), P(m+2), \ldots$ are all true. And if $P(m)$ is false, then the inductive hypothesis tells us that $P(m-1), P(m-2), \ldots$ are all false.

We are given that $P$ should be false for some integer. Call this integer $r$ . By the reasoning in the previous paragraph, we see that $P(r), P(r-1), P(r-2), \ldots$ are all false. And of course, $P(0), P(1), P(2), \ldots$ are all true. So that leaves the integers $r+1, r+2, \ldots, -2, -1$ . We don’t know if $P$ holds for these numbers. But there is only a finite list of these numbers, so there must be some least number among them for which $P$ is true, or else $P$ is false for all of them. To see this, visualize the number line $\ldots, -1, 0, 1, \ldots$ and then visualize below that the list $\ldots, P(-1), P(0), P(1), \ldots$ . The latter list looks like …, false false false, ?, ?, …, ?, ?, true, true true, … . Either all of the question marks turn out to be false, or one of the question marks will be the smallest one which turns out to be true. (If this still confuses you, consider the following: take some children and line them up by their birth date. Either all of the children are girls, or there will be a boy, in which case one of the boys will be the youngest.) If all of the question marks are false, then the set $\{n \in \mathbf Z : P(n)\}$ is equal to $\{n \in \mathbf Z : n \geq 0\}$ . If one of the question marks turns out to be true, call the smallest one $m$ . Then by the reasoning in the previous paragraph, everything to the right of $m$ (including $m$ ) is true, and everything to the left is false (since $m$ is the least number for which $P(m)$ is true). So the set $\{n \in \mathbf Z : P(n)\}$ is equal to $\{n \in \mathbf Z : n \geq m\}$ .

So a reasonable new candidate for a necessary condition is the following: if $P$ is a solution to the exercise, then $\{n \in \mathbf Z : P(n)\}$ is equal to $\{n \in \mathbf Z : n \geq m\}$ for some integer $m$ . Is this sufficient? No, because if our set was $\{n \in \mathbf Z : n \geq 5\}$ it wouldn’t be true for all natural numbers! So we must restrict $m \leq 0$ . Now is it a sufficient condition? Let’s try to prove it. Let $m \leq 0$ and suppose $P$ is a property such that $P(n) \iff n \geq m$ . We want to show that such a $P$ is a solution to the exercise. For the base case, we see that $P(0)$ is true since $0 \geq m$ . Now suppose $P(n)$ is true. Thus $n \geq m$ , and since $n{{+}\!{+}} \geq n$ , we see that $n{{+}\!{+}} \geq m$ , so $P(n{{+}\!{+}})$ is true. Finally, we must show that $P$ is false for some integer. Easy, just take $m-1$ .

What have we shown? We’ve shown that the properties $P$ which are a solution to this exercise are precisely those for which there exists an integer $m \leq 0$ such that $P(n) \iff n \geq m$ . Of course, $P(n)$ might not look like $n \geq m$ , but it must secretly encode such a relation. An example of this is $P(n) \iff n+n \geq n$ which is equivalent to just $n\geq 0$ .

Here’s a slightly different way to think about this exercise: suppose you have a bunch of cards labeled “FF”, “FT”, and “TT”. Your goal is to create an infinite line (extending both to the left and right) from these cards, but there are three rules: (1) there must be at least one F in the line; (2) the line must have an infinite number of Ts going off to the right; and (3) when you place a new card you place it either to the left or right of the existing line, and one of the letters on the new card has to match an existing letter (except for the very first time you place a card), where if you place a card to the right the left side of the new card must match the right end of the line, and if you place a card to the left the right side of the new card must match the left end of the line. An example should help. Suppose you start by placing TT. Then to the right of it you place another TT, so that the line looks like TTT (think of the matching letter as being covered up). Then to the left of the line you place FT, so the line looks like FTTT. And so on. What must the line look like, once you have placed an infinite number of cards? It must look like …FFFFTTTT… .

Model solution

Consider $P(n)$ defined as “ $n$ is non-negative”. By trichotomy of integers, $0$ is not negative, so $P(0)$ is true. Also if $n$ is non-negative, then $n{{+}\!{+}}$ is non-negative. Finally, $P$ is false for $-1$ .

4 thoughts on “Exercise 4.1.8”

Pingback: Exercise 4.4.2 | Tao Analysis Solutions
Diego says:

July 5, 2022 at 9:05 pm

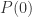What about $P(-1) \implies P(0)$ ? This is false, as $P(-1)$ is false and $P(0)$ is true. Thus, for the proposition $P(n): n \text{ is non-negative}$ we do not have 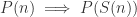$P(n) \implies P(S(n))$ for all integers.

LikeLike

1. Diego says:
  
  July 5, 2022 at 9:14 pm
  
  Never mind. $P(-1) \implies P(0)$ is true.
  
  LikeLike
2. Issa Rice says:
  
  July 5, 2022 at 9:15 pm
  
  A false statement implies anything, so that implication is actually a true statement; it’s an example of a vacuous truth.
  
  LikeLike