Exercise statement
Prove Corollary 4.1.9.
Corollary 4.1.9 (Cancellation law for integers). If 
are integers such that 
and 
is non-zero, then 
.
Hints
- There are two ways to do this. One is to use Proposition 4.1.8 to conclude that
must be zero. Another way is to combine Corollary 2.3.7 with Lemma 4.1.5.
How to think about the exercise
This is a straightforward exercise.
Model solution 1 (using Proposition 4.1.8)
Let be integers such that is non-zero. Suppose . Then we can add 
to both sides of the equation to get
. (*)
The right side of this equation (*) is 
by Proposition 4.1.6 (specifically, adding the negation of a number). To compute the left side of this equation (*), we first note that by Exercise 4.1.3, we have 
. By Proposition 4.1.6 (specifically, associativity of multiplication), we have 
. And again by Exercise 4.1.3 we have 
. Chaining these equalities together, we have that 
. Now we can compute the left side of (*). We have 
, where the last step uses Proposition 4.1.6 again (specifically, the distributive property). The left and right sides of (*) are equal, so combining our two computations, we have 
. Since 
, we can use Proposition 4.1.8 to conclude that 
. Adding 
to both sides, we have 
. By Proposition 4.1.6 again this implies 
.
(Thanks to Nam for pointing out a flaw in an earlier version of the proof. This flaw has now been fixed in the proof shown above.)
Model solution 2 (using Corollary 2.3.7 and Lemma 4.1.5)
Let be integers such that is non-zero, and suppose . Since 
are integers, there exist natural numbers 
such that 
and 
. Also since is non-zero, by trichotomy of integers (Lemma 4.1.5) it is of the form 
or 
for some positive natural number 
.
Suppose first that 
. Then the equation gives us
which simplifies to 
, i.e. 
. By the distributive law (Proposition 2.3.4), we have 
. Since 
, we can use cancellation (Corollary 2.3.7) to get 
, i.e. 
.
Now we do the case where 
. The equation gives us
which simplifies to 
, i.e. 
. This is exactly what we had in the earlier case, so the rest is exactly the same.
Tao Analysis Solutions 
I think your solution 1 is not right, since we can’t have ac + –(bc) = ac + (–b)c, and following c*(a+ (-b)) at the moment.
LikeLike
Is your objection that we are not allowed to say
? If so, this follows pretty easily from the laws of algebra: we have 
and 
. To compute 
we have 
, and so 
, so 
. So we have shown that both 
and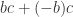 
are equal to zero. Now we can add 
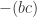to each to get the result.
There might be an easier way to show that. I kinda assumed this result was already known at this point in the book, but as I quickly scan the book now I don’t see it, so I think you are correct to point this out as an oversight on my part. If you are satisfied with my explanation above, I will edit it into the post.
LikeLike
Thinking a bit more, I found an easier way. At this point in the book we can assume the result of Exercise 4.1.3, that
for every integer 
. Using this result, we have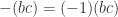 
and 
but now using the associative law for multiplication it is clear that the two are equal.
LikeLiked by 1 person
yeah I agree with your latest idea, it is brilliant! so we can have -(bc) = (-1) * bc via ex-4.1.3, then = ((-1) * b)c via prop-4.1.6 = (-b)c, via ex-4.1.3 again.
LikeLike
Ok cool, I’ve edited the post now.
LikeLike