Exercise statement
Let be a non-empty subset of
, let
be an integer, and let
be integers. Suppose
is an upper bound for
, but that
is not an upper bound for
. Without using Theorem 5.5.9, show that there exists an integer
such that
is an upper bound for
, but that
is not an upper bound for
.
Hints
- Prove by contradiction, and use induction.
- It may help to draw a picture of the situation.
How to think about the exercise
I think this is a pretty tricky exercise, if you decide to go the induction route (as suggested in the book, and as in model solution 1 below).
If you go the route of model solution 1, the tricky things are:
- When using induction, you have to realize that you shouldn’t induct on
(which is the obvious choice), but instead on the difference
.
- The inductive statement
must bring in the universal quantifiers over all
and
. If we don’t do this, then during the inductive step, we have both
and
, which is nonsense. In other words, if we fix
outside the inductive statement
, then we can’t pretend that the difference
keeps changing.
As can be seen in model solution 1, a direct proof is possible. Model solutions 2 and 3 prove by contradiction, so they are probably the sorts of proof that Tao had in mind.
Model solution 1
Let be the statement “for all integers
, if
,
is an upper bound for
, and
is not an upper bound for
, then there exists an integer
such that
is an upper bound for
and
is not an upper bound for
”. We will induct on
to show that
is true for all natural numbers
.
For the base case we have . Let
be two integers such that
, and such that
is an upper bound for
and
is not an upper bound for
. We will show that choosing
will work. Indeed,
since
. Also,
is an upper bound for
, while
is not an upper bound for
. Thus we have found an integer, and we conclude that
is true.
Now suppose inductively that is true. We want to show that
is also true. Let
be two integers such that
, and where
is an upper bound for
and
is not an upper bound for
. We have two cases, depending on whether or not
is an upper bound for
.
- Suppose first that
is not an upper bound for
. Then
so we may apply the inductive hypothesis to conclude that there exists an integer
such that
is an upper bound for
and
is not an upper bound for
. But
, so we have
, which means this same
will work.
- Now suppose that
is an upper bound for
. Then we may take
. Indeed we have
and also
so
, which means
(since
is a natural number). Thus we have
. Also,
is an upper bound for
while
is not.
In both cases, we have shown that such an integer exists, so this closes the induction.
We have shown that is true for all
. Now we need to show that the actual result holds. Let
be integers. Then
is a positive integer, so
is true. Thus we are given an integer
with the properties we want.
Model solution 2
Suppose for sake of contradiction that there is no such that
and where
is an upper bound for
and
is not an upper bound for
. We can rewrite this statement in the following form: for all
such that
, if
is an upper bound for
then
is an upper bound for
.
Now the idea is to start at and go down. Since
and
is an upper bound for
, we see that
is an upper bound for
. Continuing, we have
and know that
is an upper bound for
, so
is also an upper bound for
. We keep going until we reach
, and conclude that
is an upper bound for
, which is a contradiction.
To do this rigorously, we use induction. Let be the statement “if
, then
is an upper bound for
”. For the base case, we already showed above that
is an upper bound for
.
Now suppose inductively that is true. We must show that
is true. So suppose
. Then
so the antecedent for
is true. Thus by inductive hypothesis, we see that
is an upper bound for
. But now this means that
is an upper bound for
(by using the statement in the first paragraph of this proof). This shows that
is true, which closes the induction.
So is true for all natural numbers
. Since we assumed that
, we have
, so
is a natural number. Thus
is true. This says that if
, then
is an upper bound for
. We have
, so indeed
. Thus
is an upper bound for
, a contradiction.
Model solution 3
Suppose for sake of contradiction that there is no such that
and where
is an upper bound for
and
is not an upper bound for
.
We will show by induction on that
is an upper bound for
for all natural numbers
.
For the base case, we see that is an upper bound for
by assumption.
Now suppose inductively that is an upper bound for
. We want to show that
is an upper bound for
. By assumption
is not an upper bound for
so there exists some
such that
. Since
is an upper bound for
, we have
. Thus
. Since
is a natural number we have
. Thus
. If
were not an upper bound for
, then putting
would give an integer such that
and where
is an upper bound while
is not, a contradiction. Thus we see that
is an upper bound for
. This closes the induction.
Since , we have that
is a natural number. Thus
is an upper bound for
by what we said above, a contradiction.
Model solution 4
This is one of those problems where it is much easier to use the well-ordering principle (which is equivalent to induction but doesn’t appear until later in this book). The proof of equivalence between mathematical induction and the well-ordering principle does not require any results from analysis, so there is no circularity if we use the well-ordering principle. I’ll show it here so you get an idea of how clean the solution can be (compared to the above three solutions). I will try to remember to point back to here when I get to the well-ordering principle in the book.
Define the set
This set is non-empty since . Also,
is a lower bound for
since
for all
. Thus by the well-ordering principle there is a minimum element
. By definition of minimum element,
so
is an upper bound for
. If
were an upper bound for
then since
is not there is some
such that
. Thus
. We also have
so
. Thus
, which shows that
. But this contradicts the fact that
is the minimum element of
.
Why can’t we just argue by contradiction.
We suppose for the sake of contradiction that such an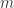 doesn’t exist, then for all
doesn’t exist, then for all 
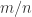 is an upper bound for
is an upper bound for 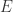 , or for all
, or for all 
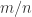 is not an upper bound for
is not an upper bound for 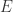 .
. satisfies the required properties.
satisfies the required properties. satisfies the required properties.
satisfies the required properties.
The first case contradicts that
The second case contradicts that
What is the need of induction in both Model answer 2 and 3 ?
LikeLike
Your negated statement is incorrect. The correct negation is presented in the first paragraph of Model solution 2.
LikeLike
I mean why use induction, if we can use the fact that the logical negation of quantifier with some statement
quantifier with some statement  is the
is the  quantifier with not
quantifier with not  .
.
LikeLike