Exercise statement
Let . Show that if
and
are eventually
-close, then
is bounded if and only if
is bounded.
Hints
- Use the triangle inequality.
How to think about the exercise
This exercise is similar to both Exercise 5.1.1 and Exercise 5.2.1. I don’t have anything to add beyond what I said in those posts.
Model solution
Suppose and
are eventually
-close, and suppose
is bounded. Since
is bounded, there exists a number
such that
for all
. Since
and
are eventually
-close, there exists
such that
for all
. By the triangle inequality we have
(to get this, you can start with the ordinary triangle inequality
and then substitute
and
), so
for all
. This bounds the sequence
(i.e. the infinite tail of
). By Lemma 5.1.14, the finite sequence
is also bounded, say by the number
. Thus we can take
as a bound on
.
For the other direction, just interchange and
in the above.
Do you think it would be possible to pick an arbitrary ? I proved it letting
? I proved it letting  . The reasoning is all the same, but you end up with
. The reasoning is all the same, but you end up with  .
.
I don’t think it should matter as you are saying that it is still bounded, but just picking bigger s ; i.e.,
s ; i.e.,  bigger than the
bigger than the 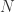 such that the distance between
such that the distance between 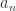 and
and  is 1.
is 1.
Also, how did you write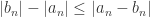 ? By strictly applying
? By strictly applying  you shouldn’t get any minus signs right? I mean I still got it to work following an approach similar to 5.2.1 and writing
you shouldn’t get any minus signs right? I mean I still got it to work following an approach similar to 5.2.1 and writing 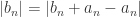 and then, applying the triangle inequality.
and then, applying the triangle inequality.
LikeLike
You are not allowed to take to be a specific number like
to be a specific number like 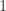 , since the exercise is to show that the claim works for an arbitrary
, since the exercise is to show that the claim works for an arbitrary  (that’s what the “Let
(that’s what the “Let 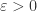 ” bit is doing in the exercise statement).
” bit is doing in the exercise statement).
To get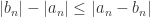 , you can start with the ordinary triangle inequality
, you can start with the ordinary triangle inequality  and then substitute
and then substitute 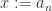 and
and  . I’ll edit the post to add this reasoning in; thanks for bringing it to my attention.
. I’ll edit the post to add this reasoning in; thanks for bringing it to my attention.
LikeLike
Ok, the triangle inequality is clearly fine the way you did it. However, I am still confuse from the first bit.
Indeed one thing that confused me was why the exercise stated: “Let . Show that if
. Show that if 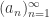 and
and  are eventually
are eventually  -steady … Why write this instead of writing that the two sequences are equivalent? After all if they are equivalent they are clearly eventually
-steady … Why write this instead of writing that the two sequences are equivalent? After all if they are equivalent they are clearly eventually  -steady for all
-steady for all  . What is the purpose of writing the sentence as Tao did? It seems to make sense only if the two sequences are not equivalent; i.e., if there is an
. What is the purpose of writing the sentence as Tao did? It seems to make sense only if the two sequences are not equivalent; i.e., if there is an  such that the two sequences do not get closer than that. Maybe I am missing something here?
such that the two sequences do not get closer than that. Maybe I am missing something here?
On a separate note, I am still not happy as to why letting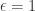 does not work. After all if choose an
does not work. After all if choose an  such that the distance between
such that the distance between 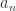 and
and  s is less than 1, and note that all
s is less than 1, and note that all 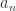 s are bounded by some
s are bounded by some  , then all the
, then all the  s must also be bounded by the same
s must also be bounded by the same  plus the maximum distance they have from the
plus the maximum distance they have from the 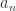 s which is
s which is 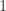 for that particular
for that particular 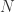 . I don’t see what is the problem with this reasoning. At the end I want to prove that the
. I don’t see what is the problem with this reasoning. At the end I want to prove that the 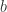 sequence is bounded, and I do conclude that. Obviously this is nitty gritty details, as I understand the proof with an arbitrary
sequence is bounded, and I do conclude that. Obviously this is nitty gritty details, as I understand the proof with an arbitrary  , but it just seems that it should also work for a given
, but it just seems that it should also work for a given  . Let me know what you think.
. Let me know what you think.
LikeLike
I thought about this some more and have a better idea of what the confusion might be about.
If we rewrite the exercise statement using first-order logic notation, we get:
where the domain of quantification is the set of positive rational numbers,
of positive rational numbers,  is the statement that the two sequences are eventually
is the statement that the two sequences are eventually  -close, and
-close, and 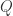 is the statement that the two sequences are either both bounded or both unbounded.
is the statement that the two sequences are either both bounded or both unbounded.
This is not the same as , which is the statement “if the two sequences are equivalent, then one is bounded iff the other one is”.
, which is the statement “if the two sequences are equivalent, then one is bounded iff the other one is”.
The above statement can be rewritten in a different way:
is equivalent to
is equivalent to
is equivalent to
is equivalent to
(Let me know if any of the above steps don’t make sense, and I can explain.)
The last statement above is still not the statement you showed: if one wants to prove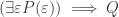 and assumes the hypothesis
and assumes the hypothesis  , one must work with the assumption that there is some non-specific
, one must work with the assumption that there is some non-specific  that makes
that makes  true, rather than setting
true, rather than setting  to be some concrete value.
to be some concrete value.
The statement you proved is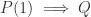 . This establishes
. This establishes  . By doing logic manipulations similar to the above we can show that this is logically equivalent to
. By doing logic manipulations similar to the above we can show that this is logically equivalent to  . So actually, you ended up showing “if the two sequences are equivalent, then one is bounded iff the other one is”.
. So actually, you ended up showing “if the two sequences are equivalent, then one is bounded iff the other one is”.
As long as the domain of quantification, namely , is non-empty,
, is non-empty,  (or equivalently
(or equivalently 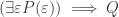 ) implies
) implies  (or equivalently
(or equivalently  ). So the exercise statement implies what you proved, but the reverse is not true.
). So the exercise statement implies what you proved, but the reverse is not true.
You are correct though that if all we care about is proving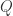 , then showing
, then showing  is sufficient.
is sufficient.
LikeLike
Here’s another way to think about this. In general, when proving a statement of the form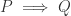 , the weaker the hypothesis statement
, the weaker the hypothesis statement 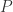 is, the stronger the overall implication is. So in this problem,
is, the stronger the overall implication is. So in this problem, 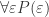 is the strongest hypothesis, because it implies
is the strongest hypothesis, because it implies  and
and  . But if we compare
. But if we compare  and
and  , then actually
, then actually  is stronger because it implies
is stronger because it implies  (but not the other way around). So this exercise is getting us to prove
(but not the other way around). So this exercise is getting us to prove 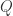 starting from the weakest of these three hypotheses, which results in the strongest implication, which is the most “interesting” statement.
starting from the weakest of these three hypotheses, which results in the strongest implication, which is the most “interesting” statement.
LikeLike
Well, I must say that I agree with you now. I think that what I did is misread Tao’s question. In particular I was thinking of
However, Tao most probably does not mean this as this would mean (as you correctly point out) that the two sequences are equivalent. However, he is very careful in not stating that.
Now it also much clearer why is clearly sufficient to show
is clearly sufficient to show 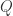 , it is simply not sufficient to show
, it is simply not sufficient to show  , which makes sense.
, which makes sense.
This was a rather insightful discussion. Thanks a lot.
LikeLike
Glad I was able to help! 🙂
LikeLike
Thanks for the solution.
Can you please say why we’re showing the below in the proof? is also bounded, say by the number
is also bounded, say by the number  . Thus we can take
. Thus we can take 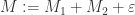 as a bound on
as a bound on  .”
.”
“By Lemma 5.1.14, the finite sequence
especially why do we need two M’s to show that it’s bounded since we can easily say that it is bounded because it’s finite?
LikeLike
One part of the sequence is bounded because it’s finite. Another part of the sequence is bounded because we proved some bound for it. How do we know that the entire sequence is bounded? The definition of “bounded sequence” does not allow you to say “well, one part is bounded by one thing, and another part is bounded by another thing, so the whole sequence is bounded”. Instead, you must produce a single bound for the entire sequence. There are multiple ways of producing such a bound, but some common ways are to add the two separate bounds or to take the max of the separate bounds.
I’m not entirely sure I answered your question. If I didn’t, please say some more words about what seems confusing.
LikeLiked by 1 person
After some thought, now I guess I understand. , there’s no guarantee that
, there’s no guarantee that  starts at zero, which imply the existence of a finite sequence of
starts at zero, which imply the existence of a finite sequence of  where
where  . if at all such finite sequence exists, then by lemma 5.1.14, it is bounded (by some
. if at all such finite sequence exists, then by lemma 5.1.14, it is bounded (by some  ).
). (or)
(or)  as the bound for the entire
as the bound for the entire  sequence.
sequence.
Though we’d found that
From here, like you said, we can take either
Please let me know if this reasoning is correct.
LikeLike
That sounds right, except that holds for all
holds for all  . So it is
. So it is 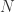 (rather than
(rather than  ) that we can’t be sure is
) that we can’t be sure is  (the sequences in this exercise start at
(the sequences in this exercise start at  rather than zero).
rather than zero).
For the max bound, using would be semantically clearer (we are saying “make it a number that’s as big as each of the two bounds we found”), although the bound you gave also works.
would be semantically clearer (we are saying “make it a number that’s as big as each of the two bounds we found”), although the bound you gave also works.
LikeLiked by 1 person
Got it, I actually found those errors (n starts at 1 and not at 0) just after submitting the reply but couldn’t edit it. Also, I see that the latex is not rendering properly for some time, I wonder whether that’s usual or I’d need to add the latex quote – “ around the symbols.
However, your answer clarifies everything.
Thanks for your time! 🙂
LikeLike
That happens because I manually fix up the LaTeX, since otherwise it’s hard for me to read the comment 😛
On WordPress blogs like this one, you can write LaTeX by writing $latex \sin x$ for example (i.e. like normal LaTeX except that you have to also write “latex” after the beginning dollar sign). You can find more documentation here.
LikeLiked by 1 person