Exercise statement
Show that the definition of negation on the integers is well-defined in the sense that if , then
(so equal integers have equal negations).
Hints
- Review the proof of Lemma 4.1.3 and try to write a similar proof.
How to think about the exercise
This is a straightforward exercise that tests your ability to write a correct proof that something is well-defined.
Model solution
Let be natural numbers, and suppose
. By definition of negation (definition 4.1.4), we have
and
. To show that
we must show that
. But we already know that
, which means that
. But now
equals
by commutativity of addition (proposition 2.2.4), which equals
from what we said above, which equals
by commutativity of addition again.
Another solution would be to use the transitive property of the equivalence relation of integers (since it has been already proved earlier near the definition 4.1.1).
In order for the definition to be well-defined, it should be independent of the choice of representatives of an equivalence class.
So, let’s say (a, b) ~ (a’, b’). That means, they both belong to the same equivalence class. Then the definition that uses both of them should be equal. i.e, D(a, b) = D(a’, b’) where D represents a definition.
So, here, we need to prove -(b, a) = -(b’, a’)
W.k.t -(b, a) ~ (a, b) and -(b’, a’) ~ (a’, b’).
Also, from our above assumption, (a, b) ~ (a’, b’).
By, using the transitive property, we can say that -(b, a) ~ -(b’, a’).
Which is the same as -(b, a) = -(b’, a’) since they both represent the same equivalence class.
@IssaRice can you please review if the above proof?
Thanks!
LikeLike
I am confused. In your notation, we want to show that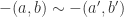 rather than what you have shown, which is
rather than what you have shown, which is  .
.
LikeLike
Oops, sorry! Looks like I’d reversed the definition of negation.
Like, (a, b) = – (b, a) rather than defining as (b, a) = – (a, b).
Should have added this at the start of the proof.
@IssaRice Would this work now?
LikeLike
So we have by assumption. We also have
by assumption. We also have 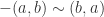 and
and 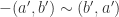 by the definition of negation. I don’t see how to use these three equivalences to show that
by the definition of negation. I don’t see how to use these three equivalences to show that 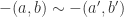 . It seems like we’d need to know that
. It seems like we’d need to know that 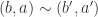 , but showing this requires showing
, but showing this requires showing 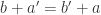 , which is what I did in my proof. Can you write down your full proof again?
, which is what I did in my proof. Can you write down your full proof again?
LikeLike
Okay, now I realise where it went different.
If we agree on the definition used in the book, – (a, b) = (b, a), then I’d assumed (b, a) ~ (b’, a’) instead of assuming (a, b) ~ (a’, b’).
I’ll rewrite the proof below:
Definition: – (a, b) = (b, a)
Assuming (a, b) ~ (a’, b’). Prove that, – (a, b) = – (a’, b’).
The above is the same as proving (b, a) = (b’, a’).
By using the symmetric property of the equivalence relation, we can write (a, b) ~ (b, a) and (a’, b’) ~ (b’, a’).
Hence we have (b, a) ~ (b’, a’) which is the same as (b, a) = (b’, a’).
The only difference is that this uses the symmetric property of equivalence relation whereas your proof uses the commutative property of addition defined for Natural numbers.
@IssaRice please let me know if there’s something wrong here. Thanks!
LikeLike
I’m still not getting your proof. As far as I know, and
and  are false, since e.g.
are false, since e.g.  is not in general equal to
is not in general equal to  . So that step of your proof does not make sense to me.
. So that step of your proof does not make sense to me.
LikeLike
You’re right! So, symmetric property says that,
if (a, b) ~ (c, d), then (c, d) ~ (a, b). But doesn’t say (a, b) ~ (b, a).
Thanks a lot for taking the time to point this out! Otherwise, would have believed in something that’s wrong. I must have been more careful.
LikeLiked by 1 person