Exercise statement
Show that the principle of induction (Axiom 2.5) does not apply directly to the integers. More precisely, give an example of a property 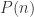 pertaining to an integer
pertaining to an integer  such that
such that 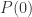 is true, and that
is true, and that 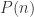 implies
implies  for all integers
for all integers  , but that
, but that 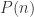 is not true for all integers
is not true for all integers  . Thus induction is not as useful a tool for dealing with the integers as it is with the natural numbers. (The situation becomes even worse with the rational and real numbers, which we shall define shortly.)
. Thus induction is not as useful a tool for dealing with the integers as it is with the natural numbers. (The situation becomes even worse with the rational and real numbers, which we shall define shortly.)
Hints
I can’t think of a good hint for this exercise. Try reading the next section paragraph by paragraph (stopping after each paragraph to attempt the exercise again).
How to think about the exercise
Exercises that ask you to find an example come with an associated extra question of “What must the solution space look like?” Is there some simple characterization of every property 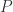 that works as a solution to this exercise? Another way to think about this is to ask the following: for any
that works as a solution to this exercise? Another way to think about this is to ask the following: for any 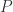 that is a solution to this exercise, what does
that is a solution to this exercise, what does 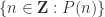 look like? Let’s try to think this through.
look like? Let’s try to think this through.
First, if 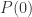 is true, and if
is true, and if 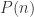 implies
implies  for all integers
for all integers  , then it must also be the case that
, then it must also be the case that 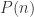 implies
implies  for all natural numbers
for all natural numbers  . So any
. So any 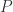 that we give must be true for all natural numbers.
that we give must be true for all natural numbers.
But we also know that 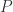 cannot hold for all integers. In other words, we want to find a
cannot hold for all integers. In other words, we want to find a 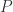 that holds for all natural numbers, but where there is also a negative integer
that holds for all natural numbers, but where there is also a negative integer 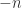 such
such  is false. This is a necessary condition, but not necessarily a sufficient condition. Is it also a sufficient condition? It is not: consider
is false. This is a necessary condition, but not necessarily a sufficient condition. Is it also a sufficient condition? It is not: consider  “
“ is not equal to
is not equal to  ”. This is true for all natural numbers and fails for
”. This is true for all natural numbers and fails for  , but it also fails the inductive hypothesis, since for
, but it also fails the inductive hypothesis, since for  , we see that
, we see that 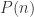 does not imply
does not imply  .
.
So we want some stronger necessary condition, which we hope will also be a sufficient condition. It’s not obvious what thought to think next. So let’s just think concretely. We already know  must all be true. What about
must all be true. What about  ? Well, that could be true or false. What if it’s true? Then the inductive hypothesis says that
? Well, that could be true or false. What if it’s true? Then the inductive hypothesis says that 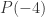 is true, so
is true, so  must be true, and so on. Once we get to
must be true, and so on. Once we get to 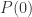 , we already know that the rest is true. What if
, we already know that the rest is true. What if  is false? Could
is false? Could 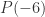 be true? No, because if
be true? No, because if 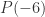 then the inductive hypothesis tells us
then the inductive hypothesis tells us  is true! So if
is true! So if  is false, then
is false, then 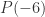 is also false, which means
is also false, which means 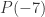 is also false, and so on.
is also false, and so on.
Generalizing the previous paragraph, let 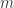 be an integer. If
be an integer. If 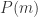 is true, then the inductive hypothesis says that
is true, then the inductive hypothesis says that 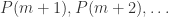 are all true. And if
are all true. And if 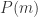 is false, then the inductive hypothesis tells us that
is false, then the inductive hypothesis tells us that  are all false.
are all false.
We are given that 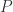 should be false for some integer. Call this integer
should be false for some integer. Call this integer  . By the reasoning in the previous paragraph, we see that
. By the reasoning in the previous paragraph, we see that  are all false. And of course,
are all false. And of course,  are all true. So that leaves the integers
are all true. So that leaves the integers 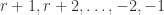 . We don’t know if
. We don’t know if 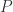 holds for these numbers. But there is only a finite list of these numbers, so there must be some least number among them for which
holds for these numbers. But there is only a finite list of these numbers, so there must be some least number among them for which 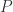 is true, or else
is true, or else 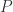 is false for all of them. To see this, visualize the number line
is false for all of them. To see this, visualize the number line 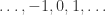 and then visualize below that the list
and then visualize below that the list  . The latter list looks like …, false false false, ?, ?, …, ?, ?, true, true true, … . Either all of the question marks turn out to be false, or one of the question marks will be the smallest one which turns out to be true. (If this still confuses you, consider the following: take some children and line them up by their birth date. Either all of the children are girls, or there will be a boy, in which case one of the boys will be the youngest.) If all of the question marks are false, then the set
. The latter list looks like …, false false false, ?, ?, …, ?, ?, true, true true, … . Either all of the question marks turn out to be false, or one of the question marks will be the smallest one which turns out to be true. (If this still confuses you, consider the following: take some children and line them up by their birth date. Either all of the children are girls, or there will be a boy, in which case one of the boys will be the youngest.) If all of the question marks are false, then the set 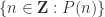 is equal to
is equal to 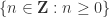 . If one of the question marks turns out to be true, call the smallest one
. If one of the question marks turns out to be true, call the smallest one 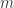 . Then by the reasoning in the previous paragraph, everything to the right of
. Then by the reasoning in the previous paragraph, everything to the right of 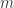 (including
(including 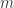 ) is true, and everything to the left is false (since
) is true, and everything to the left is false (since 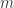 is the least number for which
is the least number for which 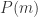 is true). So the set
is true). So the set 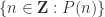 is equal to
is equal to  .
.
So a reasonable new candidate for a necessary condition is the following: if 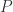 is a solution to the exercise, then
is a solution to the exercise, then 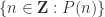 is equal to
is equal to  for some integer
for some integer 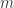 . Is this sufficient? No, because if our set was
. Is this sufficient? No, because if our set was  it wouldn’t be true for all natural numbers! So we must restrict
it wouldn’t be true for all natural numbers! So we must restrict 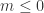 . Now is it a sufficient condition? Let’s try to prove it. Let
. Now is it a sufficient condition? Let’s try to prove it. Let 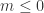 and suppose
and suppose 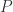 is a property such that
is a property such that 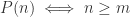 . We want to show that such a
. We want to show that such a 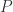 is a solution to the exercise. For the base case, we see that
is a solution to the exercise. For the base case, we see that 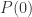 is true since
is true since 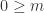 . Now suppose
. Now suppose 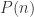 is true. Thus
is true. Thus 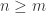 , and since
, and since 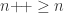 , we see that
, we see that  , so
, so  is true. Finally, we must show that
is true. Finally, we must show that 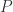 is false for some integer. Easy, just take
is false for some integer. Easy, just take  .
.
What have we shown? We’ve shown that the properties 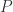 which are a solution to this exercise are precisely those for which there exists an integer
which are a solution to this exercise are precisely those for which there exists an integer 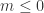 such that
such that 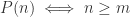 . Of course,
. Of course, 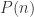 might not look like
might not look like 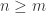 , but it must secretly encode such a relation. An example of this is
, but it must secretly encode such a relation. An example of this is  which is equivalent to just
which is equivalent to just  .
.
Here’s a slightly different way to think about this exercise: suppose you have a bunch of cards labeled “FF”, “FT”, and “TT”. Your goal is to create an infinite line (extending both to the left and right) from these cards, but there are three rules: (1) there must be at least one F in the line; (2) the line must have an infinite number of Ts going off to the right; and (3) when you place a new card you place it either to the left or right of the existing line, and one of the letters on the new card has to match an existing letter (except for the very first time you place a card), where if you place a card to the right the left side of the new card must match the right end of the line, and if you place a card to the left the right side of the new card must match the left end of the line. An example should help. Suppose you start by placing TT. Then to the right of it you place another TT, so that the line looks like TTT (think of the matching letter as being covered up). Then to the left of the line you place FT, so the line looks like FTTT. And so on. What must the line look like, once you have placed an infinite number of cards? It must look like …FFFFTTTT… .
Model solution
Consider 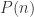 defined as “
defined as “ is non-negative”. By trichotomy of integers,
is non-negative”. By trichotomy of integers,  is not negative, so
is not negative, so 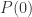 is true. Also if
is true. Also if  is non-negative, then
is non-negative, then 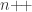 is non-negative. Finally,
is non-negative. Finally, 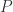 is false for
is false for  .
.
,
, and
be real numbers. Then, with the above definition of equality for real numbers, we have
. Also, if
, then
. Finally, if
and
, then
.
we need to show that
is equivalent to
. So let
. Then for
we have
for every
, so
as desired.
implies
, suppose
and
are equivalent. This means that for every
there is some
such that for all
we have
. By Proposition 4.3.3(d) we know that
, so the above is actually also saying that
and
are equivalent. More formally, let
. Then by the equivalence of
and
we are given some
. Then for
we have
.
and
. This means that
and
are equivalent, and that
and
are equivalent. Let
be given. Then there exists
such that
is
-close to
for all
, and there exists
such that
is
-close to
for all
. So if we pick
then for
we have both
and
. Thus by Proposition 4.3.7(c) we see that
and
are
-close. Thus
as required.